Singular Value Decomposition #
Singular Value Decomposition (SVD) is a powerful matrix factorization technique that plays a crucial role in various fields, including machine learning, signal processing, and data analysis.
At its core, SVD decomposes a real or complex matrix into three matrices: two orthogonal matrices and one diagonal matrix containing the singular values.
The beauty of SVD lies in its ability to capture the essential information within a matrix while filtering out noise or less significant components. This property makes SVD an invaluable tool for applications such as data compression, dimensionality reduction, and low-rank approximations. One notable application of SVD is in the field of natural language processing, where it is used in techniques like Latent Semantic Analysis (LSA) to uncover the underlying semantic relationships between words and documents. Similarly, in computer vision and image processing, SVD is employed for tasks like image compression (e.g., JPEG) and watermarking.
The SVD of a matrix $A$ ($m \times n$) is given by:
$$ A = U \Sigma V^T $$
Where:
- $A$ is an $m \times n$ matrix
- $U$ is an $m \times m$ orthogonal matrix ($U^T U = I$)
- $\Sigma$ (Sigma) is an $m \times n$ diagonal matrix with non-negative real numbers on the diagonal
- $V^T$ is the transpose of an $m \times m$ orthogonal matrix $V$ ($V^T V = I$)
The diagonal entries of $\Sigma$ are called the singular values of $A$, denoted by $\sigma_i$:
$$ \Sigma = \begin{bmatrix} \sigma_1 & 0 & \cdots & 0 \ 0 & \sigma_2 & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & \sigma_r \end{bmatrix} $$
Where $r$ is the rank of $A$, and the singular values are arranged in descending order:
$$ \sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r \geq 0 $$
The columns of $U$ and $V$ are called the left and right singular vectors of $A$, respectively:
$$ U = \begin{bmatrix} | & | & & | \ u_1 & u_2 & \cdots & u_m \ | & | & & | \end{bmatrix} $$
$$ V = \begin{bmatrix} | & | & & | \ v_1 & v_2 & \cdots & v_n \ | & | & & | \end{bmatrix} $$
The singular values in $\Sigma$ are arranged in descending order, and they represent the importance or “energy” of each corresponding pair of singular vectors in $U$ and $V$. The larger singular values capture more important information about the original matrix A, while smaller singular values capture less important or “noisy” information.
The SVD can be expressed in terms of the sum of rank-1 matrices:
$$ A = \sum_{i=1}^r \sigma_i u_i v_i^T $$
Where $u_i$ and $v_i$ are the i-th columns of $U$ and $V$, respectively. The low-rank approximation of $A$, using the top $k$ singular values and vectors, is given by:
$$ A_k = \sum_{i=1}^k \sigma_i u_i v_i^T $$
Where $A_k$ is the best rank-k approximation of $A$ in the least-squares sense.
How the SVD is computed #
- Calculate the matrix product $A^T A$, which is an $m \times m$ matrix.
- Find the eigenvalues and eigenvectors of $A^T A$.
- The eigenvectors of $A^T A$ are the columns of $V$.
- The singular values $σ_i$ are the square roots of the eigenvalues of $A^T A$.
- The columns of $U$ are obtained by multiplying $A$ with the corresponding columns of $V$, and then dividing by the corresponding singular values.
Mathematically, it can be expressed as:
$$ A^T A = V \Lambda V^T $$
Where $\Lambda$ is a diagonal matrix containing the eigenvalues of $A^T A$. The singular values $σ_i$ are the square roots of the diagonal elements of $\Lambda$:
$$ \Sigma = \sqrt{\Lambda} $$
And the columns of U are given by:
$$ U = A V \Sigma^{-1} $$
Visualizing SVD and Low-Rank Matrix Approximation #
This script extends the visualization by comparing different ranks of matrix approximations. It quantifies the approximation quality using the Frobenius norm, providing a clear metric to evaluate how well each low-rank approximation represents the original matrix.
"""
This script generates a random 10x10 matrix, computes its SVD, and visualizes both the original matrix and its rank-2 approximation. It also prints the matrices to the console.
"""
import numpy as np
import matplotlib.pyplot as plt
# Generate a random matrix A of size 5x3
A = np.random.randn(10, 10)
# Compute the SVD
U, s, Vh = np.linalg.svd(A, full_matrices=False)
# Rank for low-rank approximation
k = 2 # Choose a smaller value for k to see the effect
# Low-rank approximation
sigma_k = np.diag(s[:k])
U_k = U[:, :k]
Vh_k = Vh[:k, :]
A_approx = U_k @ sigma_k @ Vh_k
# Plot the original matrix
plt.figure(figsize=(8, 4), dpi=200)
plt.subplot(1, 2, 1)
plt.imshow(A, cmap='viridis')
plt.title('Original Matrix')
plt.colorbar()
# Plot the low-rank approximation
plt.subplot(1, 2, 2)
plt.imshow(A_approx, cmap='viridis')
plt.title(f'Rank {k} Approximation')
plt.colorbar()
plt.tight_layout()
plt.show()
print("Original matrix:\n", A)
print(f"\nLow-rank approximation (rank {k}):\n", A_approx)
Example Output #
Assessing Approximation Quality with Frobenius Norm #
Calculates the error between the original matrix and its approximations for different ranks. This error is the Frobenius norm of the difference between the original and approximated matrices, normalized by the Frobenius norm of the original matrix.
"""
Performs SVD on a random matrix, visualizes low-rank approximations, and computes approximation errors.
The script generates a random 10x10 matrix, computes its SVD, and creates visualizations for different rank approximations. It also calculates and prints the Frobenius norm of the error for each approximation.
"""
import numpy as np
import matplotlib.pyplot as plt
# Generate a random matrix
A = np.random.randn(10, 10)
# Compute the SVD
U, s, Vh = np.linalg.svd(A, full_matrices=False)
# Low-rank approximations
ranks = [1, 3, 6, 9]
errors = []
fig, axes = plt.subplots(2, 2, figsize=(8, 6), dpi=200)
axes = axes.flatten() # Flatten the axes into a 1D array
for rank, ax in zip(ranks, axes):
sigma = np.diag(s[:rank])
A_approx = U[:, :rank] @ sigma @ Vh[:rank, :]
im = ax.imshow(A_approx, cmap='viridis')
ax.set_title(f'Rank {rank} Approximation')
fig.colorbar(im, ax=ax) # Add colorbar to the current axis
error = np.linalg.norm(A - A_approx) / np.linalg.norm(A)
errors.append(error)
plt.tight_layout()
plt.show()
print("Errors for different ranks:")
for rank, error in zip(ranks, errors):
print(f"Rank {rank}: {error:.4f}")
Example output #
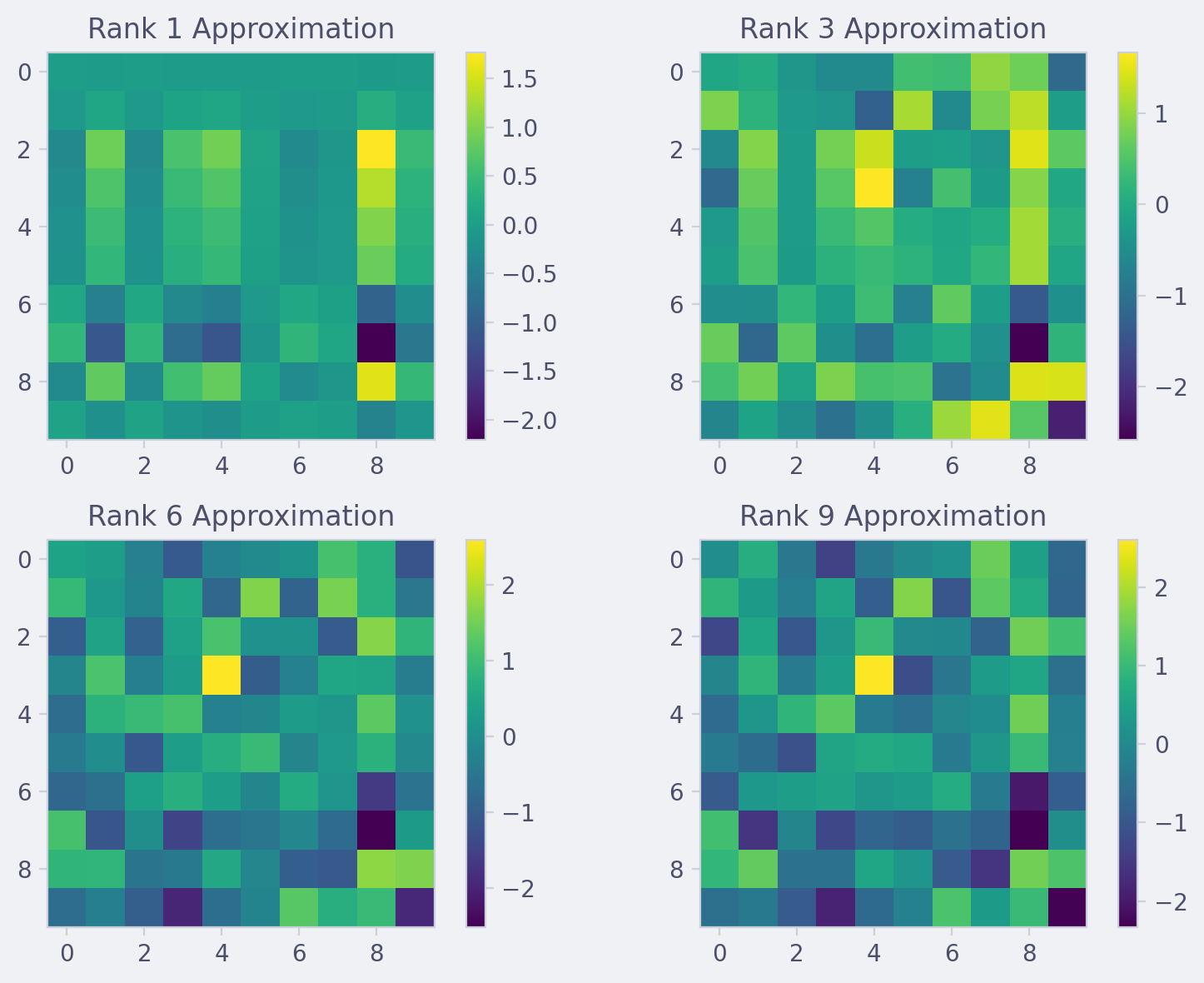
Errors for different ranks:
Rank 1: 0.8228
Rank 3: 0.5732
Rank 6: 0.2730
Rank 9: 0.0550
Important properties and applications #
Low-rank approximation: By keeping only the k largest singular values and their corresponding singular vectors, we can approximate the original matrix $A$ as $A \approx U_k \Sigma_k V_k^T$, where $U_k$, $\Sigma_k$, and $V_k^T$ are the truncated matrices containing the top $k$ singular values and vectors. This is known as the low-rank approximation of $A$, and it is useful for data compression, noise reduction, and dimensionality reduction.
- Matrix inversion and pseudoinverse: The SVD can be used to compute the inverse or pseudoinverse of a matrix, which is useful in linear algebra and least-squares problems.
- Data analysis and dimensionality reduction: The SVD is used in techniques like Principal Component Analysis (PCA) and Latent Semantic Analysis (LSA) for dimensionality reduction and data analysis.
- Image compression and processing: The SVD is used in image compression algorithms like JPEG and in various image processing tasks, such as watermarking and noise removal. Signal processing: The SVD is used in signal processing applications like signal denoising, feature extraction, and subspace tracking.
LoRA Merging #
SVD is used to perform a low-rank approximation of the merged LoRA weights. By keeping only the top $k$ singular values and vectors, the script extracts a low-rank representation of the merged weights, which can be more efficient and compact than the original merged weights. This low-rank representation is then used as the new LoRA weights for the merged model.
The truncation of singular values and vectors is controlled by the --new_rank and --new_conv_rank arguments, which specify the desired rank (or dimension) of the output LoRA model.
The script also applies clamping to the singular vectors to prevent them from becoming too large or too small, which can help improve numerical stability and convergence during training or fine-tuning.
Alternatives and Comparisons #
While SVD is a powerful and versatile matrix factorization technique, several alternatives exist, each with its own strengths, weaknesses, and appropriate use cases.
Eigenvalue Decomposition (EVD) #
Eigenvalue Decomposition (EVD) is closely related to SVD and is often used for dimensionality reduction techniques like Principal Component Analysis (PCA). However, EVD is only applicable to square matrices, while SVD can handle rectangular matrices. EVD decomposes a square matrix into a set of eigenvectors and eigenvalues, providing a different perspective on the matrix structure compared to SVD.
Non-negative Matrix Factorization (NMF) #
Non-negative Matrix Factorization (NMF) is particularly useful for data that naturally has non-negative values, such as images, text documents, and audio signals. Unlike SVD, NMF enforces non-negativity constraints on the factorized matrices, which can lead to more interpretable factors or representations. However, NMF may not always provide the optimal low-rank approximation compared to SVD, and its performance can be sensitive to initialization and parameter settings.
Tensor Decompositions #
For higher-order data (tensors), CANDECOMP/PARAFAC (CP) and Tucker decomposition can be used as alternatives to SVD. These techniques can capture multi-way interactions and provide dimensionality reduction for tensors, enabling applications in areas such as chemometrics, neuroimaging, and signal processing.
Randomized Algorithms and Sparse Matrix Factorizations #
Randomized algorithms, such as the Randomized SVD and Randomized Tensor Decompositions, can provide efficient approximations of SVD and tensor decompositions, respectively. These algorithms are particularly useful for large-scale matrices or tensors, where exact decompositions may be computationally expensive. For sparse matrices, techniques like Sparse PCA, Sparse SVD, and Sparse Coding can be used to obtain sparse factor representations, which can be beneficial for interpretation and compression.
Deep Learning-based Methods #
With the rise of deep learning, several techniques have emerged for dimensionality reduction and matrix factorization using neural networks. Examples include Autoencoders, Variational Autoencoders (VAEs), and Generative Adversarial Networks (GANs). These methods can learn non-linear representations and can be more flexible than traditional matrix factorization techniques like SVD. However, they often require large amounts of training data and can be more computationally expensive compared to SVD.
The choice of technique ultimately depends on the specific problem, data characteristics, computational constraints, and desired properties of the factorization or dimensionality reduction method.
Interpreting Singular Vectors #
While the singular values provide a clear measure of the importance or energy associated with each singular vector pair, interpreting the singular vectors themselves can be challenging, especially in high-dimensional spaces. The singular vectors may not always have an intuitive interpretation, making it difficult to extract meaningful insights or perform further analysis based on them.
One strategy to aid in the interpretation of singular vectors is to examine their components or loadings. In certain applications, such as text mining or image processing, the components of the singular vectors may correspond to specific features or patterns that can be interpreted based on domain knowledge. Additionally, visualization techniques like heat maps, biplots, or embedding projections can be employed to gain insights into the structure and relationships encoded in the singular vectors.
Another approach is to combine SVD with other techniques or domain-specific constraints. For example, in natural language processing, incorporating linguistic knowledge or word embeddings can help interpret the singular vectors in a more meaningful way. In computer vision, imposing sparsity or non-negativity constraints on the singular vectors can lead to more interpretable representations.
Computational Complexity and Numerical Stability #
Computing the SVD of a large matrix can be computationally expensive, especially for dense matrices. The computational cost grows significantly with the size of the matrix, making it challenging to apply SVD to very large-scale problems. The time complexity of the SVD algorithm for an $m \times n$ matrix is $O(\min(m^2n, mn^2))$, which can become prohibitive for large matrices.
To address this limitation, various approximation techniques and algorithms have been developed to reduce the computational burden. One popular approach is the Randomized SVD, which uses random projections to approximate the singular values and vectors efficiently. Other techniques include iterative methods, such as the Lanczos algorithm, and parallel or distributed implementations of SVD.
Numerical stability is another important consideration when computing SVD. Ill-conditioned matrices, round-off errors, and numerical precision limitations can introduce instabilities and inaccuracies in the computed singular values and vectors. To mitigate these issues, techniques like pivoting, scaling, and iterative refinement are often employed. Additionally, as mentioned in the post, clamping the singular vectors to prevent them from becoming too large or too small can improve numerical stability and convergence during training or fine-tuning in certain applications.
"""
This script benchmarks the computational cost and numerical stability of Singular Value Decomposition (SVD) on random matrices of various sizes
"""
import numpy as np
import time
def svd_condition_benchmark(matrix_sizes):
"""
This function generates random matrices of specified sizes and computes their SVD to determine the elapsed time for the computation and the condition number for each matrix. The condition number is calculated as the ratio of the largest to the smallest singular value, which indicates the numerical stability of the matrix.
Parameters:
matrix_sizes (list of tuples): A list of tuples where each tuple contains two integers representing the number of rows and columns (m, n) of the matrix to be generated and benchmarked.
Returns:
list of tuples: Each tuple contains two floats representing the elapsed time in seconds and the condition number for the corresponding matrix size.
Raises:
np.linalg.LinAlgError: If SVD computation fails due to matrix properties.
"""
results = []
for m, n in matrix_sizes:
A = np.random.rand(m, n)
start_time = time.time()
try:
U, s, Vh = np.linalg.svd(A, full_matrices=False)
condition_number = s[0] / s[-1]
end_time = time.time()
elapsed_time = end_time - start_time
results.append((elapsed_time, condition_number))
print(f"Matrix size ({m}, {n}): {elapsed_time:.6f} seconds, Condition number = {condition_number:.6f}")
except np.linalg.LinAlgError as e:
print(f"Error for matrix size ({m}, {n}): {e}")
continue
return results
# Benchmark for computational cost and numerical stability
matrix_sizes = [(100, 100), (500, 500), (1000, 1000), (2000, 2000), (5000, 5000)]
benchmark_results = svd_condition_benchmark(matrix_sizes)
Historical Background #
The origins of Singular Value Decomposition (SVD) can be traced back to the early 20th century, with contributions from mathematicians like Eugenio Beltrami, Camille Jordan, and James Joseph Sylvester. However, the modern formulation and widespread adoption of SVD are largely attributed to the works of Gene Golub and William Kahan in the 1960s. Their seminal paper, “Calculating the Singular Values and Pseudo-Inverse of a Matrix,” introduced efficient computational methods for SVD and laid the foundation for its numerous applications in various fields.
Conclusion #
Singular Value Decomposition (SVD) is a powerful and versatile matrix factorization technique with numerous applications across various fields. While it has certain limitations and challenges, such as computational complexity, numerical stability, and interpretability of singular vectors, researchers and practitioners continue to develop strategies and techniques to mitigate these issues. By combining SVD with other methods, incorporating domain-specific knowledge, or leveraging approximation algorithms, the power of SVD can be harnessed effectively for a wide range of tasks, from data compression and dimensionality reduction to signal processing and pattern recognition.